Recherche du nombre d'or dans l'ensemble de Mandelbrot
Vous allez sur cette page, après quelques observations guidées, constater encore un fois la présence du nombre d'or dans l'ensemble de Mandelbrot, mais dans une nouvelle région.
La région que nous allons explorer ici se trouve sur la gauche de l'ensemble de Mandelbrot. Nous allons redéfinir dans cette région un "circuit de têtes", c'est à dire numéroter différentes têtes que nous explorerons dans l'ordre de leur numéro. Attention, ce circuit n'ayant aucun rapport avec le premier circuit que nous avons explorer à la page précédente, les têtes que nous numérotons ici n'ont rien à voir avec les têtes précédentes (exemple : ce que nous appellerons ici la tête n°3 N'EST PAS LA TÊTE N°3 DU PREMIER CIRCUIT). En effet, il y a des milliers de façons pour numéroter les têtes, et donc de définir "un circuit de têtes", le numéro d'une tête n'est donc pas absolu.
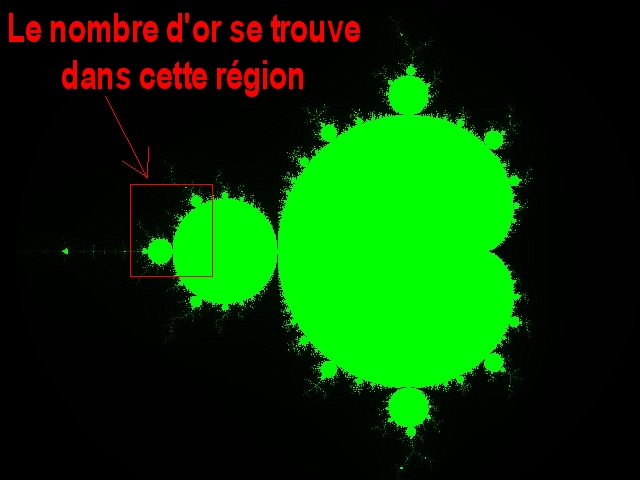
Définissons les 2 premières têtes du circuit que nous allons explorer :

Un fois qu'on a définit les deux premières têtes, il est très facile de repérer toutes les autres têtes du circuit. Il faut pour cela appliquer toujours le même principe de repérage, qui est le suivant :
La tête n°k est la plus grosse tête située entre la tête n°k-1 et la tête n°k-2
On peut alors repérer et explorer toutes les têtes du circuit, en "avançant" dans le circuit.
Repérage des têtes n°3 à n°7 :
Appliquons le principe de repérage pour trouver les têtes n°3 à n°7.
La tête n°3 est la plus grosse tête entre les têtes 2 et 1 :

La tête n°4 est la plus grosse tête entre les têtes 3 et 2 :

La tête n°5 est la plus grosse tête entre les têtes 4 et 3 :

La tête n°6 est la plus grosse tête entre les têtes 5 et 4 :
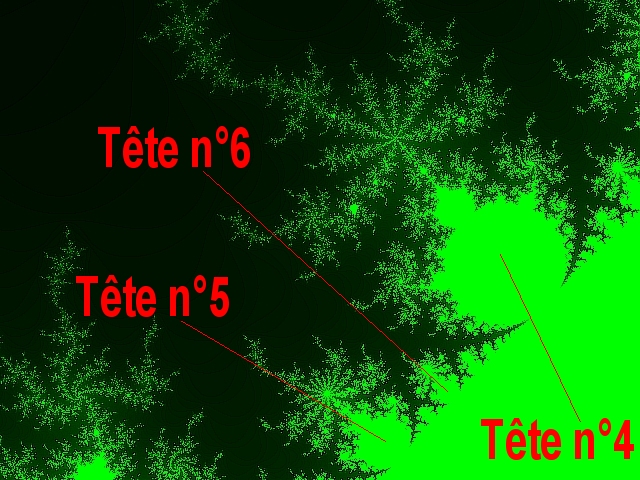
La tête n°7 est la plus grosse tête entre les têtes 6 et 5 :
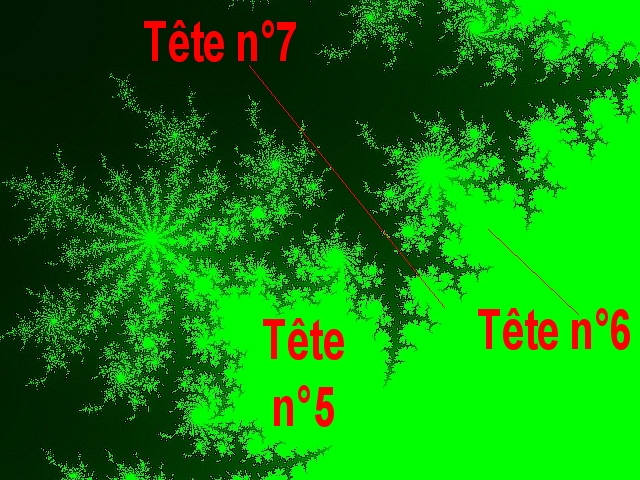
Et on pourrait continuer ainsi pour repérer toutes les autres têtes (la tête n°8, la tête n°9, la tête n°10, etc...).
Analyse des têtes n°2 à n°7 :
Maintenant que vous savez où se trouvent les têtes n°2 à n°7 dans l'ensemble de Mandelbrot, nous allons les analyser dans le but de déterminer leur ordre et leur rang.
Rappel :
-
L'ordre d'une tête est le nombre total de branches (en comptant l'antenne principale)
-
Le rang d'une tête est le numéro de la branche la plus petite, en comptant les branches dans le sens des aiguilles d'une montre, et en finissant par l'antenne principale
Analyse de la tête n°2 :

Tête n°2
Comme la branche la plus courte porte le n°2, le rang de la tête n°2 est 2.
Comme la tête n°2 a 3 branche en tout, l'ordre de la tête n°2 est 3.
Pour chaque tête, les résultats seront présentés sous forme de tableau :
| Caractéristiques de la tête n°2 | |
| Rang | 2 |
| Ordre | 3 |
Analyse de la tête n°3 :

Tête n°3
| Caractéristiques de la tête n°3 | |
| Rang | 3 |
| Ordre | 5 |
Analyse de la tête n°4 :

Tête n°4
| Caractéristiques de la tête n°4 | |
| Rang | 5 |
| Ordre | 8 |
Analyse de la tête n°5 :

Tête n°5
| Caractéristiques de la tête n°5 | |
| Rang | 8 |
| Ordre | 13 |
Analyse de la tête n°6 :
Comme la tête n°6 possède beaucoup de branches, 2 photos sont nécessaires pour compter sans ambiguïté toutes les branches. La seconde photo représente un zoom entre les branches 8 et 16.

Tête n°6 complète

Zoom de la tête n°6, entre les branches 8 et 16
On peut voir sur cette seconde photo que la branche la plus petite est la branche n°13.
| Caractéristiques de la tête n°6 | |
| Rang | 13 |
| Ordre | 21 |
Analyse de la tête n°7 :
Comme la tête n°7 possède beaucoup de branches, 3 photos sont nécessaires pour compter sans ambiguïté toutes les branches. La seconde photo représente un zoom entre les branches 5 et 13, et la troisième photo représente un zoom entre les branches 13 et 26.

Photo de toutes les branches de la tête n°7

Zoom de la tête n°7, entre les branches 5 et 13

Zoom de la tête n°7, entre les branches 13 et 26
On peut voir sur cette troisième photo que la branche la plus petite est la branche n°21.
| Caractéristiques de la tête n°7 | |
| Rang | 21 |
| Ordre | 34 |
Récapitulation des résultats
Récapitulons l'ensemble des résultats de ces observations expérimentales dans un tableau :
| N° de la tête | Rang de la tête | Ordre de la tête |
| 2 | 2 | 3 |
| 3 | 3 | 5 |
| 4 | 5 | 8 |
| 5 | 8 | 13 |
| 6 | 13 | 21 |
| 7 | 21 | 34 |
On remarque encore une fois que le rang et l'ordre des têtes de ce circuit forment deux suites de Fibonacci, c'est à dire des suites de nombres où chaque terme est égal à la somme des deux termes précédents.
Le rang et l'ordre d'une tête étant deux termes consécutifs de la suite de Fibonacci, nous pouvons en déduire que :
Le rapport entre l'ordre et le rang d'une tête tend vers le nombre d'or lorsque le numéro de la tête tend vers l'infinie.
Exemple pour la tête n°7 : le rapport ORDRE / RANG nous donne 34 / 21=1.619, soit une première valeur approchée du nombre d'or. Pour les têtes suivantes, le rapport ORDRE / RANG se rapproche de plus en plus de la valeur exacte du nombre d'or.
Pour aller encore plus loin :
Il existe dans l'ensemble de Mandelbrot des dizaines de circuits de têtes dont le rapport ORDRE / RANG tend vers le nombre d'or lorsqu'on avance dans le circuit (c'est à dire lorsque le numéro des têtes augmente). J'en ai moi même déjà trouvé plusieurs, dont les 2 qui sont exposés ici sur mon site. En cherchant bien, vous pouvez trouvez vous-même votre propre "circuit de têtes en or", qui, peut être, n'a encore jamais été découvert pour ses liens avec le nombre d'or.
Mais les "têtes" ne sont pas les seuls objets constituant l'ensemble de Mandelbrot. On trouve aussi, en plus des têtes, des spirales, des étoiles, des "araignées", etc... Chacun ayant donné des noms différents à tous ces objets, divers et variés, que l'en retrouve en quantité et de manière récurrente (le bras d'une spirale est constitué de spirales, elles-mêmes constituées d'autres petites spirales, etc...) dans l'ensemble de Mandelbrot. On peut donc très bien définir, par exemple, des "circuits de spirales", ou des circuits permettant de passer d'un objet à un autre objet de même nature, quelque soit cet objet (tête, spirale, araignée, étoile, etc.).
Pour définir un circuit, il suffit d'indiquer les 2 premiers objets du circuit, et de définir un principe de repérage, qui permet de trouver sans ambiguïté tous les objets suivants du circuit.
Il existe donc une infinité de circuits définissables dans l'ensemble de Mandelbrot. Mais parmi tous ces circuits, quel sont ceux qui, en raison de certaines caractéristiques de leurs objets (comme l'ordre et le rang, pour les têtes) font intervenir le nombre d'or ? Voilà une question à laquelle personne n'a encore répondu, et qui occupera, j'en suis sûr, les plus curieux (et courageux) d'entre vous. Pour ma part, je vais tout de suite continuer à chercher de nouveaux circuits en or, en me remettant immédiatement à fouiller dans l'ensemble de Mandelbrot :-))
Comment créer vous-même des images fractales de qualité ?
Les images exposées sur cette page ne sont pas très nettes en raison de la compression JPEG utilisée. En revanche, elles sont rapides à télécharger. Si vous voulez obtenir des images de l'ensemble de Mandelbrot, extrêmement nettes et précises, vous pouvez vous-même créer vos propres images fractales en haute résolution, en utilisant le logiciel GECIF, et en sauvegardant les images obtenues dans un format graphique non destructeur (préférez les formats bitmap PCX ou BMP aux formats destructeurs comme le JPG ou le GIF, ces deux derniers formats ayant été conçus pour enregistrer des photos (floues par définition) et non des images de synthèse (extrêmement nettes) comme les images fractales).
Toutes les illustrations de l'ensemble de Mandelbrot exposées ici ont été réalisées avec le logiciel GECIF que j'ai programmé. Gecif est un véritable microscope électronique, qui permet d'aller voir au cœur des fractales, et d'explorer des milliers de nouveaux mondes jusqu'ici jamais explorés. Si vous aussi vous voulez partir à la découverte de l'ensemble Mandelbrot en faisant des zooms sur ses frontières pour constater de vous-même certains phénomènes, si vous voulez re-calculer en haute résolution certaines photos exposées ici, ou si vous voulez observer des têtes de l'ensemble de Mandelbrot qui ne sont pas présentées sur cette page, il vous suffit de télécharger gratuitement GECIF en cliquant ici. Gecif est un gratuiciel (un "freeware") qui s'adresse à tous ceux qui, comme moi, s'émerveille devant cet objet naturel aux curiosités inépuisables qu'est l'ensemble de Mandelbrot :-))